|
|
リレーによる 4bit 加算回路 （4bit adder） |
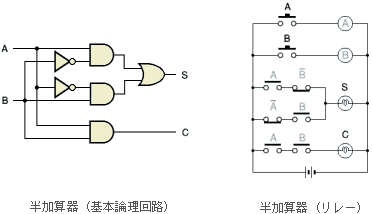
半加算器 や スイッチ（リレー）による半加算器
のページで、基本論理回路やリレーを使って半加算器を作れることが分かりました。
半加算器は 2 進数の 1 桁の足し算ができます。
しかし、2 進数の 1 桁だけでは、これが本当に使い物になるのか、少し気懸かりです。
そこで、半加算器を組み合わせて、リレーで 4 ビットの 2 進数を加算する回路を作ってみます。
複数のビットの加算をするには、下位の桁の加算で生じたキャリーも加えなくてはなりませんから、
1 桁加算するのに半加算器が 2 個必要です。
ただし、最下位の桁では下位桁からのキャリーがないので、4 ビットの加算回路では 2 × 3 ＋ 1、
計 7 個の半加算器があればいいことになります。
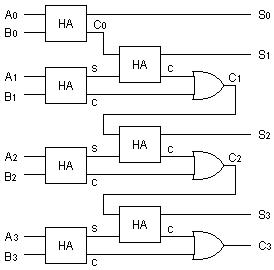
下図が加算回路です。
一見複雑そうですが、よく見れば、単に半加算器が 7 個
組み合わせられているだけ
だということが分かります。
スイッチ A0 〜 A3、
B0 〜 B3、
リレーのコイル A0 〜 A3、
B0 〜 B3、
または下部の 2 進数 A, B の付近をクリックすると動きます。
これで、 4 桁の 2 進数の加算ができますから、試してみて下さい。
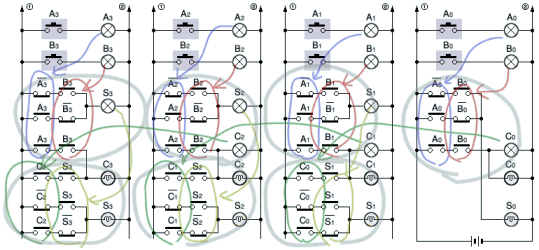
リレーを使って、実際に 4 ビットの加算回路を作ってみました。
web では試してもらえないので残念ですが、スイッチを押す度にリレーがカチカチと動いて、
まぎれもなく 「電気回路が計算している」 ことが実感できます。
リレー式 4 ビット加算回路 （0110 ＋ 0111 ＝ 1101 の計算例）
トランジスタや IC は、リレーのような 「スイッチ」 と同じ働きをしますから、
リレーで計算ができるのなら、 IC で計算ができて不思議はありません。
論理回路や演算回路、あるいはコンピュータといったようなものも、
スイッチを組み合わせていけばできるんだということが、理解しやすくなるように思えます。
リレー式の加算器は、動作速度の遅さも、大きな特徴 (?) です。
例えば、A を 1111、B を 0000 （1111 ＋ 0000 ＝ 1111 の状態）
にしておいて、B を 0001 にする （1111 ＋ 0001 ＝ 10000） と、
最下位ビットに 1 を加えたことによってキャリーが発生し、
それが次々に上位桁に波及していく様子が分かります。
目に見えるほど遅くはありませんが、複数のリレーの作動音が 「ジャッ」 という風に聞こえて、
計算に多少時間がかかっている、という雰囲気がします。
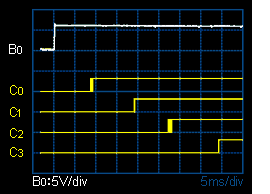
それを測定してみたのが左の図です。
A を 1111 にしておいて、B0 を 1 にすると、
まず C0 が 1 に、
ついで C0 が 1 になったために C1 が 1 に、
という風に、キャリーが上位桁に及んでいっている様子がよく分かります。
図の横軸は一目盛が 5msec ですから、キャリーはほぼ 10msec で伝わっており、
B3 が 1 になってから、ほぼ 40msec 後に C3 が 1 になっています。
4 ビットの 2 進数を加算するのに、0.04秒 かかったわけです。
もしこれが 32ビットの加算器であれば、計算に 0.3秒 かかることになります。
加算を 1 万回ほど繰り返すというようなプログラムでは、それ
（加算） だけで 1 時間近くかかってしまいます。
やはりリレーは、高速処理には向きません。
（look-ahead carry adder という、キャリーを別途計算して、高速に処理できる加算回路もあります。）
| 関連事項： | 講義資料／半加算器 講義資料／スイッチ（リレー）による半加算器 講義資料／2進数の加減算 |
|---|
*1 A0〜A3、B0〜B3 のスイッチを押すと、青、赤の線で囲まれている 3つの接点が動きます。
グレーの線で囲まれている部分それぞれが半加算器です。
また、下図は論理回路で書いた加算回路です。HA はそれぞれ半加算器を表しています。 論理的には、上の図とまったく同じです。
2005.01.24
