 |
半加算器 （half adder） |
2 進数の数字は 0 と 1 だけですから、 2 進数の加算には次の 4 種類の組み合わせしかありません。
ここで S は和、 C は加算の結果生じた桁上げ (carry) です。 10進数でも 7＋3＝10 のように、 一桁の数値どうしの加算でも桁上げが生じて 2 桁になるのと同じで、 2 進数では 1+1＝10 になります。
2 進数の数値 A、 B に対して、 上の表のように C と S を出力できるものであれば、 電気回路であろうが機械であろうが、 それは加算器として使うことができます。
たとえば基本論理回路を下図のように組み合わせると、 このような出力が得られます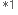
。
入力信号の記号や入力値の付近、 あるいは真理値表をマウスでクリックすると状態が変わります。
基本論理回路の真理値表を参考にして、 半加算器として動作することを確認して下さい。
上の半加算器は AND 回路、 OR 回路、 NOT 回路を使っていますが、 論理回路は同じ働きをするものをいろんな方法で作ることができます。
一例として NAND 回路 を使ったものを紹介します。 見かけは違いますが、 機能は同じです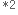
。
*1 実際に 2 進数の加算をするには、 下位の桁の計算で発生した桁上げも加えなくてはならないので、 同じものがもう一組必要になります。
この回路だけでは半分しか加算できないので 「半加算器」 といいます。
*2 半加算器演習 のページには、 もう一つ別の半加算器があります。
| A | B | C | S | ||
|---|---|---|---|---|---|
| 0 | ＋ | 0 | ＝ | 0 | |
| 0 | ＋ | 1 | ＝ | 1 | |
| 1 | ＋ | 0 | ＝ | 1 | |
| 1 | ＋ | 1 | ＝ | 1 | 0 |
ここで S は和、 C は加算の結果生じた桁上げ (carry) です。 10進数でも 7＋3＝10 のように、 一桁の数値どうしの加算でも桁上げが生じて 2 桁になるのと同じで、 2 進数では 1+1＝10 になります。
2 進数の数値 A、 B に対して、 上の表のように C と S を出力できるものであれば、 電気回路であろうが機械であろうが、 それは加算器として使うことができます。
たとえば基本論理回路を下図のように組み合わせると、 このような出力が得られます
。
|
入力信号の記号や入力値の付近、 あるいは真理値表をマウスでクリックすると状態が変わります。
基本論理回路の真理値表を参考にして、 半加算器として動作することを確認して下さい。
上の半加算器は AND 回路、 OR 回路、 NOT 回路を使っていますが、 論理回路は同じ働きをするものをいろんな方法で作ることができます。
一例として NAND 回路 を使ったものを紹介します。 見かけは違いますが、 機能は同じです
。
|
| 関連事項： 半加算器演習 リレーによる半加算器 |
*1 実際に 2 進数の加算をするには、 下位の桁の計算で発生した桁上げも加えなくてはならないので、 同じものがもう一組必要になります。
この回路だけでは半分しか加算できないので 「半加算器」 といいます。
*2 半加算器演習 のページには、 もう一つ別の半加算器があります。
update: 2012.10.04
