|
|
2進数そろばん |

![]() そういえば、いつ頃からそろばんを見かけなくなったのでしょうか。
そういえば、いつ頃からそろばんを見かけなくなったのでしょうか。
電卓が普及するにつれて姿を消していったのですが、それでも初めのうちは、
「そりゃあなた、電卓なんかよりそろばんの方がよっぽど速い」 とか、 「やっぱりこいつ(そろばん)でないとね!」
なんていう人が珍しくありませんでした。
銀行の窓口なんかにも、そばに電卓があるのに、そろばんでパチパチって、カッコいい行員さんがいたものです。
上の写真は 「そろばん電卓」![]() です。
そろばんに電卓がついているというか、電卓にそろばんがついているというべきか、
ともかくこういう商品があったということは、電卓とそろばんが共存していた時期があったことを物語っています。
です。
そろばんに電卓がついているというか、電卓にそろばんがついているというべきか、
ともかくこういう商品があったということは、電卓とそろばんが共存していた時期があったことを物語っています。
というわけで、唐突ですが、2進数と加算回路をもっと理解するために、
そろばんを使ってみようと思って 「2進数そろばん」 なるものを作ってみました。
その、「2進数そろばん」 を使うためのウォーミングアップ(復習)です。
(必要がない人はスキップして下さい。)
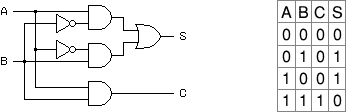
上図は、半加算回路 とその真理表です。
A と B の和、S は、A B いずれもが 0 または 1 のときは 0 で、
どちらか一方だけが 1 のときに 1 になります。
すなわち、A B 両方が 0 のときは 0 で、どちらかが 1 になると 1 になって、
そして更にA B 両方が 1になると 0 に戻ります。
また、見方を変えれば、 「A B のいずれかが変化すると、
和 S も変化する![]() 」 ともいえます。
」 ともいえます。
一方、2進数の一桁、A と B を加えることによって生じる桁上げ
(carry) C は、 A B いずれもが 1 のときに 1 になります。
上位桁の加算時に、この 1 を加えなくてはなりません。
まとめると、 1 を加えると S は変化する、
C が 1 になったら次の桁に 1 を加える といいわけです。
さて、2進数そろばんです。
ふつうの算盤は梁の上に一つ、下に四つ珠 (たま) があるのに対して、
「2進数そろばん」 の珠は一つです。
前者を 「四つ珠」 といいますが、
こちらは正真正銘の 「一つ珠」、しかも、自動そろばんです。
珠をマウスでクリックすると動きますから、試してみて下さい。
使用法:
上部の枠にある赤い三角形 ![]() は
は
![]() の位置を表しています。
(枠をクリックすると移動できます。)
の位置を表しています。
(枠をクリックすると移動できます。)
下図は、1101 + 110、すなわち 13 + 6 を計算しているところです。

動かすべき珠の位置を黒い丸印で表していますが、その珠をクリックすると左の図のようになります。
動かした結果、珠は全部上に上がります。
これに 110 を加えるには、右の図の、黒い丸印の位置の珠を動かせばいいのですが、
![]() の珠はすでに上にありますから、動かすと下に下がります。
珠が下がるということは、1 に 1 を加えて 0 になったのですから、キャリーが生じ、
上位の桁にも 1 を加えなくてはなりません。
しかし
の珠はすでに上にありますから、動かすと下に下がります。
珠が下がるということは、1 に 1 を加えて 0 になったのですから、キャリーが生じ、
上位の桁にも 1 を加えなくてはなりません。
しかし ![]() の珠も上にあるので、これも下がって、
の珠も上にあるので、これも下がって、
![]() の珠を上げることになります。
こう書くと複雑そうですが、これは 「自動そろばん」 ですから、キャリーの処理はすべて自動的に行われます。
(
の珠を上げることになります。
こう書くと複雑そうですが、これは 「自動そろばん」 ですから、キャリーの処理はすべて自動的に行われます。
(![]() ボタンをクリックすると、自動モードが解除されます。)
ボタンをクリックすると、自動モードが解除されます。)
なお、 ![]() はクリアボタンです。
はクリアボタンです。
付記 (小数について):
赤い三角形 ![]() のところは
のところは
![]() 、
その左隣は
、
その左隣は ![]() 、
そのまた左隣は
、
そのまた左隣は ![]() です。
です。
逆に、 ![]() の右隣は同様にして
の右隣は同様にして
![]() 、
その右隣は
、
その右隣は ![]() 、
そのまた右隣は
、
そのまた右隣は ![]() になります。
になります。
そしてまた、![]() は
は ![]() 、
、
![]() は
は ![]() 、
、
![]() は
は ![]() ですから、
それぞれ 0.5、0.25、0.125 という小数を表すことになります。
ですから、
それぞれ 0.5、0.25、0.125 という小数を表すことになります。
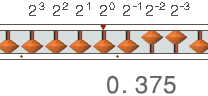
すなわち、2進数の 0.1 は 10進数の 0.5、2進数の 0.01 は 10進数の 0.25、2進数の 0.001 は 10進数の 0.125 です。
従って下図のように、2進数の 0.01 と 0.001 を加えた 0.011 は、10進数の 0.375 になります。
ところで、10進数の 0.1 は、2進数では正確に表すことができず、
その近似値は 0.00011001100110011001100 … になります。
これを 10進数で表すと 0.099999904632568359375… です。
(これは、上のそろばんで、枠の上部、白いところをクリックして
![]() を左端に移動させると計算できます。)
を左端に移動させると計算できます。)
しかしこれをもって、「なんだ、 0.1 も満足に表せないのか」 と考えるのは早計です。
10進数も、小数で ![]() を満足に表せないのです。
を満足に表せないのです。
*1 シャープ株式会社 技術本部 歴史ホール・技術ホール (〒632-8567 奈良県天理市櫟本町2613-1)
で撮影させていただきました。
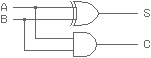
*2 半加算回路の出力 S は、
EXOR 回路と同じですから、
下図のように書くこともできます。
EXOR 回路は、入力 A B のいずれかが変わると出力も変わる性質があります。
同様の性質を持っているスイッチは、
階段の照明
などに用いられています。
![]()