|
|
チューリングマシン (Turing machine) |

Alan M. Turing
(c) National Portrait Gallery, London
チューリングマシンは無限に長いテープと、 テープに書かれている記号を読みとって内部の状態を変える自動機械 (オートマトン) からなっています。 このページではこれをヘッドと呼び、下図のようなイメージで表すことにします。
ヘッドはその内部状態と読みとった記号 (入力) に応じて、 次にテープに書くべき記号を出力し、右か左にひとつ移動して内部状態を変えます。 これを停止するまで繰り返し実行します。
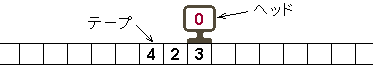
いま、ある数値をひとつだけ大きくする、つまり 1 を加えるという 「計算」 を考えてみます。
(これをインクリメント (increment) といいます。)
たとえば 423 という数字があるとき、これをひとつ大きくするためには、 まず最下位の数字を知らなくてはなりません。
ヘッドはテープに書かれた 3 の上にあってこれを読みとり、テープに 4 を書き込みます。
この場合は、仕事はこれでおしまいです。 数字が 0 なら 1、 1 なら 2、 2 なら 3、 3 なら 4… を書き込めばいいわけです。
しかしこの数字が 9 の場合は 0 を書き込み、つぎにヘッドは左に移動してとなりの数字も読みとらなくてはなりません。 上図の場合は 2 なので、これを 3 にすればいいのですが、これも 9 ならさらに左… となります。
数字がすべて 9 の場合は全部 0 に書きかえて、さらに左の空白を 1 に、 999 は 1000 にしなくてはなりません。
このように、数値をひとつ大きくするにも、条件が変われば必要な処理も変わりますが、 こうしたルール通りにヘッドが動いてテープの数字を書きかえてやればいいわけです。
下にあるのは実際に動くチューリングマシン (Java アプレット) です。
あらかじめ数値をひとつ大きくする、 インクリメントのルールを組み込んであります。
ただし、 10進数ではルールが複雑になる (0 なら 1、 1 なら 2、 2 なら 3…) ので、 ここでの数値は 2進数です。
ヘッドに表示されている 0 はヘッド (自動機械) の内部状態です。
この場合の 0 は 「さあ、 インクリメントするぞ」 というモードです。
2進数なのでルールは簡単で、 0 は 1 に、 1 は 0 にしますが、 0 を 1、 あるいは空白を 1 にしたら計算はおしまいで、 内部状態は 1、 「仕事は片づいた、元の位置に戻ろう」 モードに変わります。
元の位置に戻ると仕事は完了して 内部状態は H (停止) になります。
テープにはあらかじめ 101、 10進数にすると 5 という数字が書かれています。
現在の内部状態とテープの数字から、ヘッドがテープに書き込む記号やヘッドの移動方向、 次に内部状態がどう変わるかなどがルール表の中で赤く表示されています。
「ステップ」 というボタンをクリックする度に作業が進みます ( 「実行」 をクリックすると自動的に進んでいきます)。
内部状態が H になって停止したとき、テープは 110、 10進数の 6 に変わっています。
テープをクリックすると "入力" という名前のキーが濃くなります。 これを使ってテープの数字を書きかえることができますから、 違う数字(桁数が長くなっても構いません) に書きかえて (ヘッドはドラッグして最下位の桁まで移動させて)、 いろんな数値で試して下さい。
左上にあるポップアップメニューから、他の計算、否定や加算、減算などに変更することができます。
加算や減算はルールが複雑なので、ルール表に全部一度には表示できませんが、 条件に合致するルールは表内に赤色で表示されます。 また、ルール表を縦方向にドラッグして、隠れている部分を表示させることもできます。
減算は否定、 インクリメント、 加算を組み合わせて、 補数を使って計算しています。 まず減数 0110 を反転させて 1 の補数を作り、 これをインクリメントして 2 の補数にして加えます。 最後に最上位の 1 を消して計算を終了します。
ルール表をクリックすると、対応するキーが濃く表示されてルールを編集することもできます。
いずれは新規ルールを作成できるようにするつもりですが、現在は未対応です。
ご了承下さい。
m(._.)m

