|
|
石の数学と砂の数学（デジタル） |
ギリシャの数学には、「石の数学」 と 「砂の数学」 との二種類があったと云われている。
「石の数学」 というのは、石ころを並べて、その個数を数えてゆく数学で、数論である。
「砂の数学」 と云うのは、砂に絵を描いて行く数学で、幾何である。
つまり、石の数学はボツボツとバラバラに不連続に離れ離れになったものを取り扱っており、
これをディスクリート （discrete）（離散と訳す） と呼ぶ。
これに対して、砂の数学は連続につながっている線を取り扱うもので、
これをコンティニュー （continue）（連続と訳す） と呼ぶ。
このディスクリートがデジタルであり、コンティニューがアナログであることは云うまでもない。
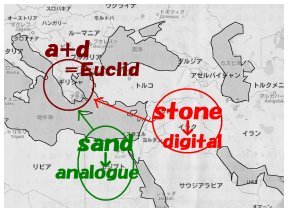
石の数学はバビロニア系で、砂の数学はエジプト系だと云う説もあるらしい。
トルコあたりの石山とエジプトの砂漠の連想から来ているもので、真偽の程はおぼつかない。
そして、このような 「石の数学」 と 「砂の数学」 という相矛盾し相対立するものを、
巧みに調和させ統合したのがユークリッドの 「幾何学原論」 であったとも云われている。
現代において、石と砂を統合させたものは
PCM （パルス符号変調） と標本化定理であると云えるのではあるまいか。
PCM は連続した線をボツボツに細かく切断して小さな点にしてしまおうと云うものである。
これによって、連続したアナログを離散したデジタルに変換するのである。
そして、離散した点は再びつなぎ合わされて、元の連続した線に戻る。
この技術によって、現代の華々しいマルチメディア世界が作られていった。
だけど、幾ら細かく裁断したところで線は線である。顕微鏡で見れば、ある長さを持っている。
本当の点にはなり得ない。そこで登場するのが標本化定理である。
これは、平易に云えば、 「ある程度細かければ実用上はそれで充分だ」 と云うものである。
考えてみれば、実にイイカゲンな話である。
現代の技術は、あるいは現代の社会は、このようなイイカゲンさの上に成り立っているのだ。
しかし、これをもって悲嘆することはあるまい。
どうせ人間と云うものは、完全無欠のものではないのだから。
特に、人間の感覚というものは、あるアイマイさの上に成り立っているのだから。
（参考文献） 森毅 「魔術から数学へ」 講談社学術文庫、1991年。