 |
平均情報量／エントロピー （entropy） |
「情報量」 のページで、
トランプのカードを 1 枚引いたらハートだったという場合、
確率は 1/4 なので、 情報量は 2bit という説明をしました。
しかしこの話は、 どのカード （スーツ） を引く確率もみな同じであることが前提です。
トランプのカードなら問題ありませんが、 次のような 「抽選」 ならどうでしょうか。
賞は 「特等」、 「1等」、 「2等」、 「外れ」 の4種類でトランプのスーツの数と同じですが、 「外れ」 の確率が大きいので、 抽選に行ってもたいていは 「外れ」 です。 はじめから結果が分かっているようなものには 0.0161 ビット、 情報量がほとんどありません。
逆に 「特等」 は文字通り万に一つ、 滅多にないことなので、 情報量も 13.288 ビット、 外れの 825 倍もあります
。
平均情報量／エントロピー電卓
トランプでは、 スペードもハートもクラブもダイヤも、 どのスートのカードを引く確率も 1/4、 情報量はすべて 2 bit です。
このときの平均情報量はもちろん 2 bit ですから、 トランプに比べると抽選の平均情報量は 1.9 bit 以上も減ってしまったわけです。
これは常識的にも納得のできる話です。
トランプのカードは何を引くか全く分かりませんが、 抽選はたいてい 「外れ」 です。
結果が初めから分かりきっているようなものには、 情報の価値はほとんどありません。
平均情報量は次の式で計算します。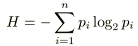
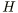は平均情報量、
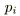は確率です。
確率の総和は 1 でないといけません （上の電卓では、 確率の総和が 1 でないときは点滅表示になります）。
上の抽選の例の場合だと、 平均情報量は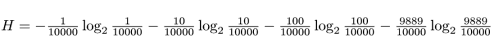
実際に計算するにも上の式を使いますが…、 見ただけでウンザリです。
計算には上の 「平均情報量電卓」 をおすすめします。
熱力学に分子の無秩序さを表す 「エントロピー（entropy）」 という言葉がありますが、 エントロピーを表す式は上式とまったく同じ形をしていますので、 平均情報量を 「エントロピー」 とも言います。
平均情報量 （エントロピー） は、 情報の無秩序さ、 あいまいさ、 不確実さを表す尺度でもあります。
ある事柄の発生確率がすべて同じとき （たとえば、トランプのカードを引くとき）、 すなわち何が起こるか予測がつかないときに最大で、 発生確率の偏りが大きければ大きいほどエントロピーは小さくなって、 ひとつの事柄の確率が 1 で他はすべて 0、 すなわち最初から結果が分かりきっている場合には最小値、 0 になります。
しかしこの話は、 どのカード （スーツ） を引く確率もみな同じであることが前提です。
トランプのカードなら問題ありませんが、 次のような 「抽選」 ならどうでしょうか。
| 賞 | 本 数 | 確 率 | 情 報 量 （bit） |
|---|---|---|---|
| 特等 | 1本 | 0.0001 | 13.2877 |
| 1等 | 10本 | 0.001 | 9.9658 |
| 2等 | 100本 | 0.01 | 6.6439 |
| 外れ | 9,889本 | 0.9889 | 0.0161 |
賞は 「特等」、 「1等」、 「2等」、 「外れ」 の4種類でトランプのスーツの数と同じですが、 「外れ」 の確率が大きいので、 抽選に行ってもたいていは 「外れ」 です。 はじめから結果が分かっているようなものには 0.0161 ビット、 情報量がほとんどありません。
逆に 「特等」 は文字通り万に一つ、 滅多にないことなので、 情報量も 13.288 ビット、 外れの 825 倍もあります
。
ところでこういう場合、 「平均情報量」 はどう考えればいいのでしょうか。
ここでも理屈は後回しにして、 まず計算してみます。
下にあるのは 「平均情報量電卓」 です。
テキストボックスの中に確率をすべて、 この場合 0.0001、0.001、0.01、0.9889 と
4 行で入力
し、 
を押します。
答えは 0.09365782 bit になります。
平均情報量／エントロピー電卓
トランプでは、 スペードもハートもクラブもダイヤも、 どのスートのカードを引く確率も 1/4、 情報量はすべて 2 bit です。
このときの平均情報量はもちろん 2 bit ですから、 トランプに比べると抽選の平均情報量は 1.9 bit 以上も減ってしまったわけです。
これは常識的にも納得のできる話です。
トランプのカードは何を引くか全く分かりませんが、 抽選はたいてい 「外れ」 です。
結果が初めから分かりきっているようなものには、 情報の価値はほとんどありません。
平均情報量は次の式で計算します。
は平均情報量、
は確率です。確率の総和は 1 でないといけません （上の電卓では、 確率の総和が 1 でないときは点滅表示になります）。
上の抽選の例の場合だと、 平均情報量は
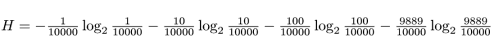
実際に計算するにも上の式を使いますが…、 見ただけでウンザリです。
計算には上の 「平均情報量電卓」 をおすすめします。
熱力学に分子の無秩序さを表す 「エントロピー（entropy）」 という言葉がありますが、 エントロピーを表す式は上式とまったく同じ形をしていますので、 平均情報量を 「エントロピー」 とも言います。
平均情報量 （エントロピー） は、 情報の無秩序さ、 あいまいさ、 不確実さを表す尺度でもあります。
ある事柄の発生確率がすべて同じとき （たとえば、トランプのカードを引くとき）、 すなわち何が起こるか予測がつかないときに最大で、 発生確率の偏りが大きければ大きいほどエントロピーは小さくなって、 ひとつの事柄の確率が 1 で他はすべて 0、 すなわち最初から結果が分かりきっている場合には最小値、 0 になります。
| 関連事項： 情報量 |
